Logaritmo
| Logaritmo | |
|---|---|
 Gráfica de Logaritmo | |
| Definición | |
| Tipo | Función real |
| Descubridor(es) | Nikolaus Mercator (1668)[1] |
| Dominio | ![]0,+\infty[](http://upload.wikimedia.org/math/e/b/8/eb8a0ceeec2805d7e3ba7c0591eafa52.png) |
| Codominio | ![]-\infty,+\infty[](http://upload.wikimedia.org/math/d/a/6/da6b9b99f9b93ed32a0cc8706361afa7.png) |
| Imagen | ![]-\infty,+\infty[](http://upload.wikimedia.org/math/d/a/6/da6b9b99f9b93ed32a0cc8706361afa7.png) |
| Propiedades | Biyectiva Cóncava Estrictamente creciente |
| Cálculo infinitesimal | |
| Derivada |  |
| Función inversa |  |
| Límites |   |
| Funciones relacionadas | Función exponencial |
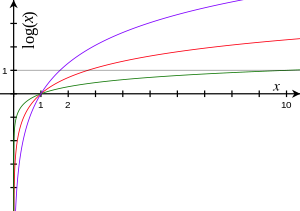
| El rojo representa el logaritmo en base e. El verde corresponde a la base 10. El púrpura al de la base 1,7. | |
En matemáticas, el logaritmo de un número en una base determinada es el exponente al cual hay que elevar la base para obtener el número. Es la función matemática inversa de la función exponencial.
Logaritmación es la operación aritmética donde dando un número resultante y una base de potenciación, se tiene que hallar el exponente al que hay que elevar la base para conseguir el mencionado resultado. Así como la suma y multiplicación tienen como operaciones opuestas la resta y la división respectivamente, la logaritmación es la operación inversa a la exponenciación.
Concepto
Dado un número real (argumento x), la función logaritmo le asigna el exponente n (o potencia) a la que un número fijo (base b) se ha de elevar para obtener dicho argumento. Es la función inversa de la exponencial x = bn. Esta función se escribe como: n = logb x, lo que permite obtener n.
(esto se lee como: logaritmo en base "b" de "x" es igual a "n"; sí y solo si "b" elevado a la "n" da por resultado a "x")
- La base b tiene que ser positiva y distinta de 1
0, b \ne 1)" src="http://upload.wikimedia.org/math/d/2/6/d2641c49bb9f288b81fcd0babccf0626.png">.
- x tiene que ser un número positivo (x > 0).
- n puede ser cualquier número real
 .
.
Así, en la expresión 102 = 100, el logaritmo de 100 en base 10 es 2, y se escribe como log10 100 = 2.
Se denomina logaritmo neperiano (ln) o logaritmo natural al logaritmo en base e; fueron desarrollados por John Napier.
Los logaritmos de base 10, decimales, comunes o vulgares son aquellos en que la base es 10. Fueron inventados y desarrollados por Henry Briggs.
Para representar la operación de logaritmación se escribe la abreviatura Log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Ejemplo: 103 = 1000 luego Log101000 = 3.
Cuando se sobreentiende la base, se puede omitir. Para indicar logaritmos en base e se usa ln.









No hay comentarios:
Publicar un comentario